魔术公式轮胎模型参数识别方法研究
2025-08-24
摘要:本文在研究Pacejka’94魔术公式轮胎模型的基础上,利用Matlab Simulink建立了Pacejka’94轮胎模型的纵向力、侧向力及回正力矩的仿真模型。以MAXXIS185-60R14-82H轮胎稳态纵滑力学特性、稳态侧偏力学特性、稳态侧倾力学特性试验数据为例,通过Matlab Simulink提供的参数估计工具箱对纵向力的14个参数、侧向力的18个参数、回正力矩的21个参数进行了估计识别。从仿真计算结果来看,估计值与试验数据值具有很好的拟合度。因此将这些识别的参数用于多体动力学软件中的Pacejka’94轮胎模型能得到较好的模型精度和仿真结果。
1
引言
2
Pacejka’94轮胎模型的力学表达[3]
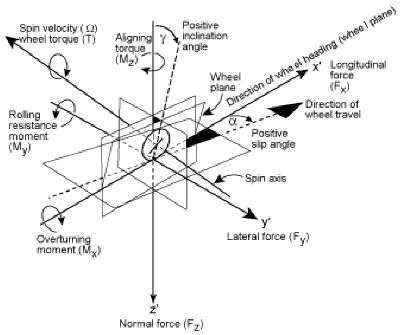
Negative in a left turn. | ||
Negative during braking. | ||
Negative in a right turn. | ||
Positive in traction. |
• 侧向力表达式:
3
Pacejka’94轮胎模型参数识别
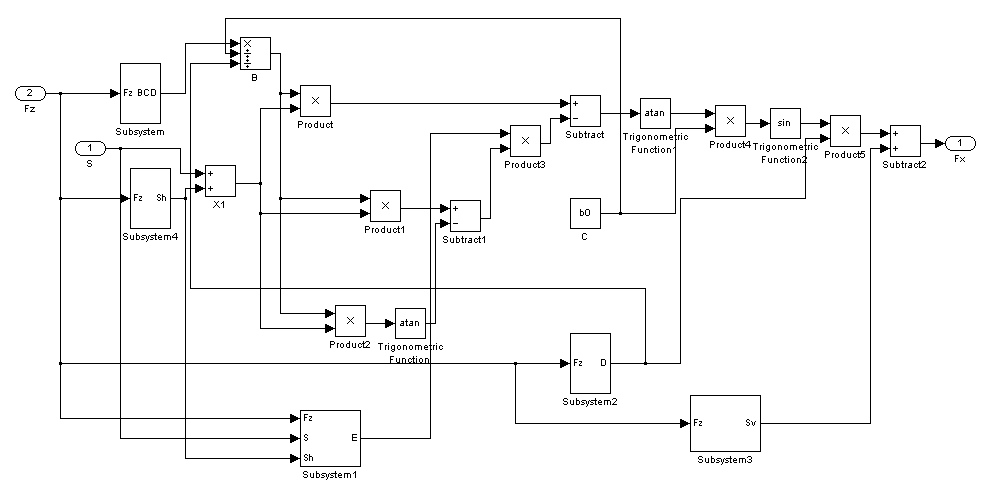
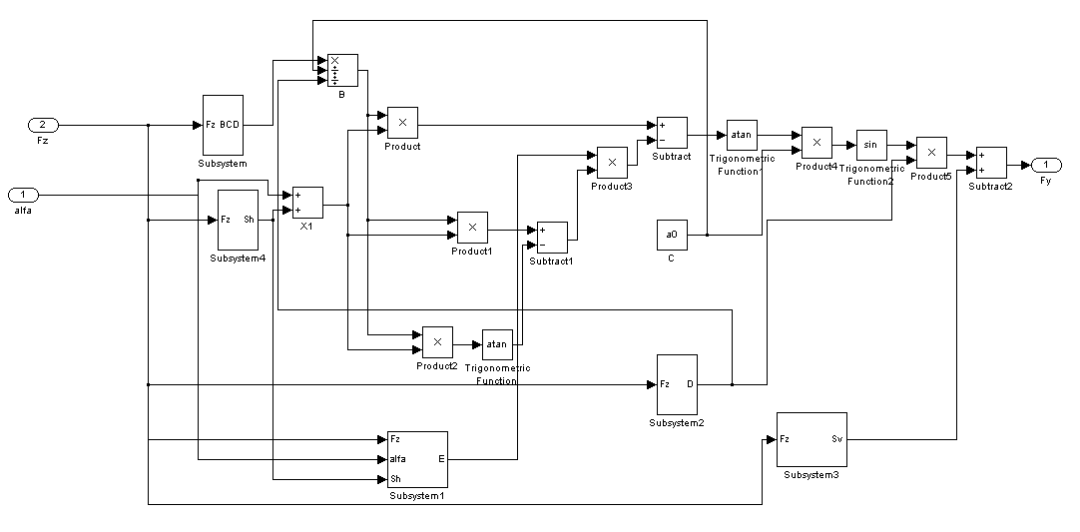
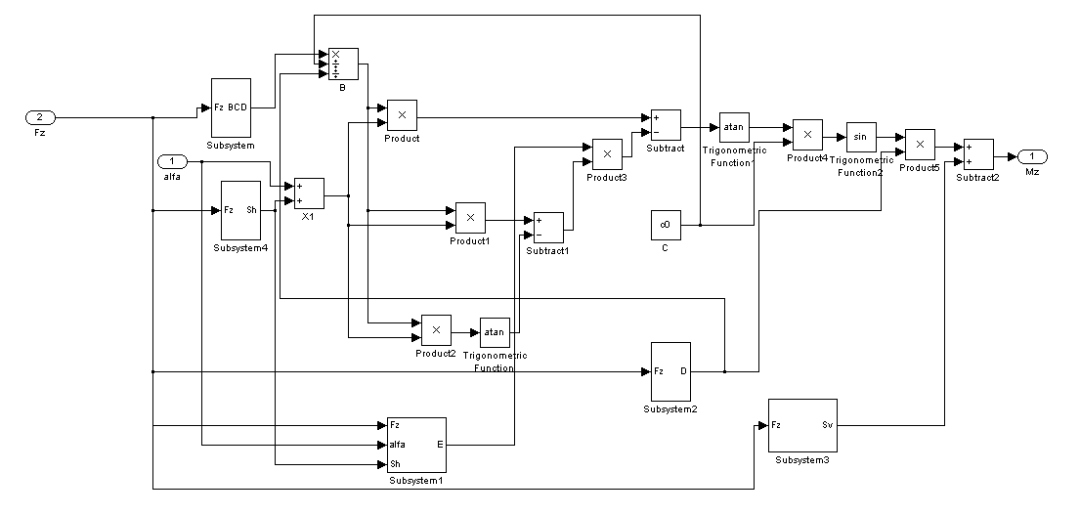
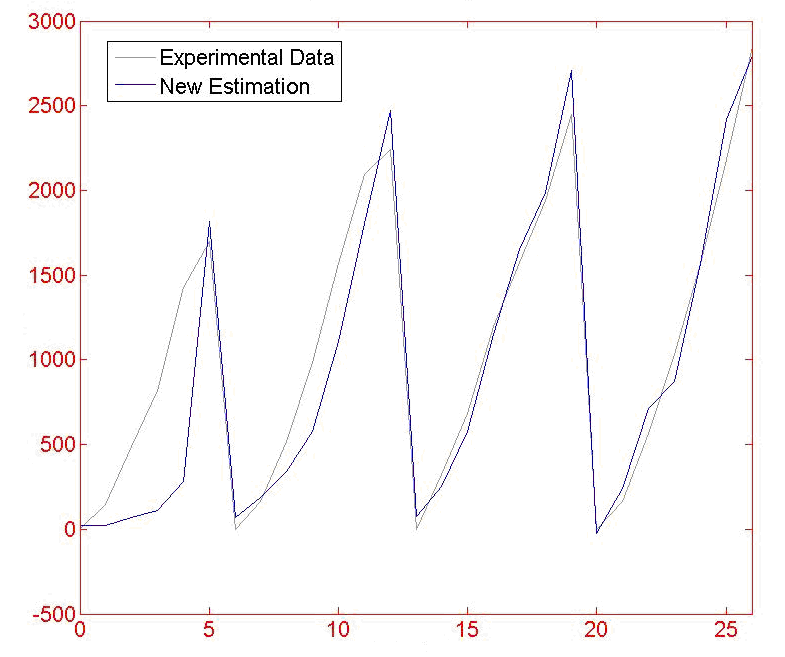
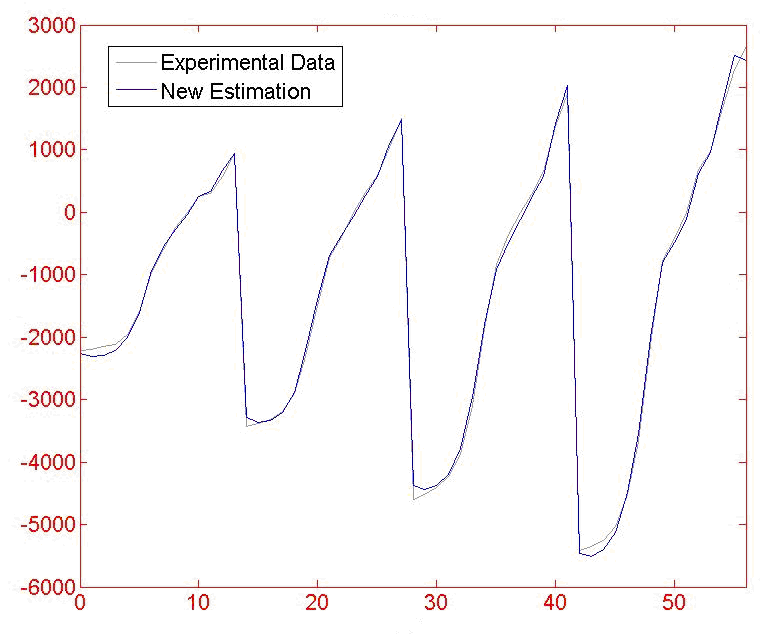
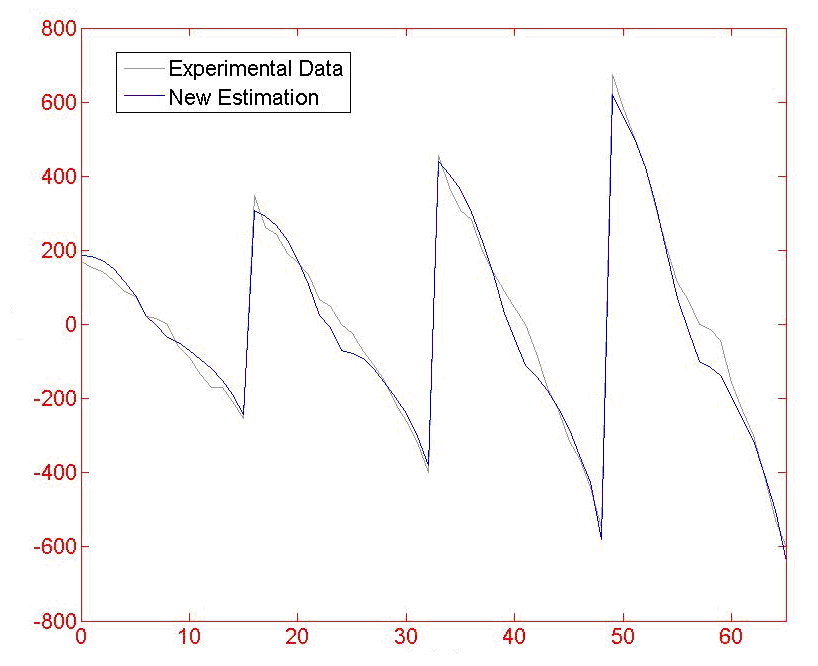
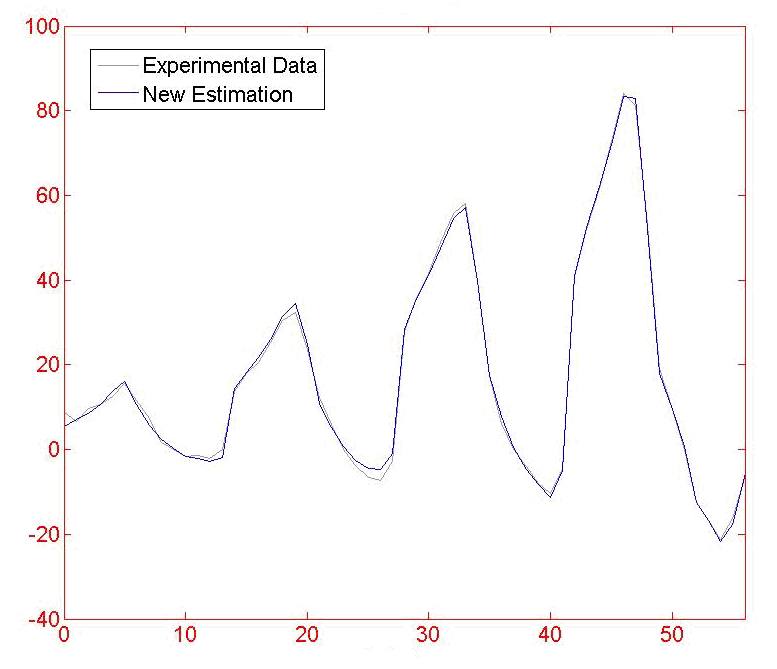
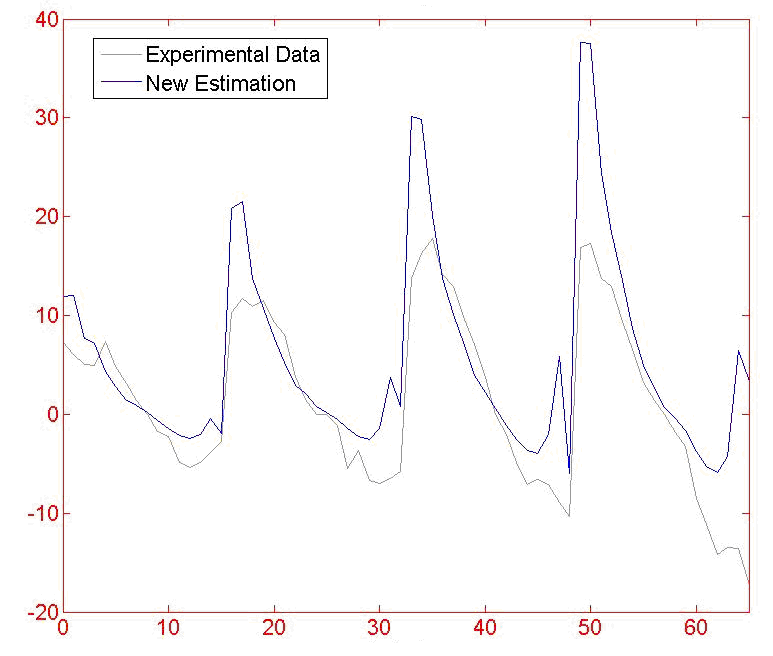
4
Pacejka’94轮胎模型属性文件
5
结论
写评论...